Ba đường conic trong mặt phẳng tọa độ Toán lớp 10

Ba đường conic trong mặt phẳng tọa độ là đường elip, hypebol và parabol. Tổng hợp lý thuyết cùng các ví dụ, bài tập vận dụng dễ hiểu.

Lý thuyết về ba đường Conic trong mặt phẳng tọa độ, bài tập vận dụng kèm lời giải đầy đủ, chi tiết. Các em học cùng techtuts theo dõi và nắm bắt ngay nội dung bài học này nhé!

Ba đường conic trong mặt phẳng tọa độ - Đường Elip

Ta cho 2 điểm cố định là F1, F2 và độ dài không đổi 2a lớn hơn F1F2. Đường Elip (E) sẽ tập hợp các điểm M trong mặt phẳng sao cho F1M + F2M = 2a.

Điểm F1, F2 được gọi là các tiêu điểm của elip.

Độ dài F1F2= 2c được gọi là tiêu cực của elip (a > c)

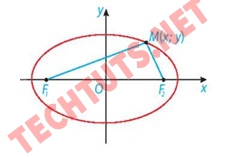
Với b = a2 - c2

Xét trong mặt phẳng Oxy, elip có 2 tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối 2 tiêu điểm đó. Từ đó ta có phương trình x^2/a^2 + y^2/b^2 = 1. Ngược lại, mỗi phương trình có dạng x^2/a^2 + y^2/b^2 = 1 với a > b > 0 đều là phương trình của elip có 2 tiêu điểm:

F1 (-a2 - b2 ; 0) và F2 (a2 - b2 ; 0)

Tiêu cực 2c = 2a2 - b2

Tổng các khoảng cách từ mỗi điểm thuộc elip tới 2 tiêu điểm bằng 2a.

Phương trình x^2/a^2 + y^2/b^2 = 1 gọi là phương trình chính tắc của elip tương ứng.

Ví dụ:

Cho 2 phương trình là (x^2 / 4^2) + (y^2 / 3^2) = 1 và (x^2 / 3^2) + (y^2 / 4^2) = 1

Ta có phương trình chính tắc của elip có dạng x^2 / a^2 + y^2 / b^2 = 1 (a > b > 0)

Như vậy phương trình chính tắc của đường elip sẽ là (x^2 / 4^2) + (y^2 / 3^2) = 1.

Xem thêm: Số nguyên tố là gì? Tính chất và cách tìm số nguyên tố

Ba đường conic trong mặt phẳng tọa độ - Đường Hypebol

Với 2 điểm phân biệt cố định F1 và F2 ta đặt F1F2 = 2c và cho số thực dương a nhỏ hơn c.

Tập hợp các điểm M sao cho |MF1 - MF2| = 2a được gọi là đường hypebol. F1, F2 được gọi là 2 tiêu điểm và F1F2 = 2c được gọi là tiêu cự của hypebol đó.

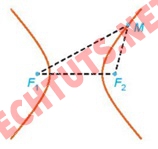
Lưu ý: Hypebol có 2 nhánh, 1 nhánh gồm những điểm M sao cho MF1 - MF2 = 2a. Còn lại là những điểm M sao cho MF1 - MF2 = -2a.

Xét trong mặt phẳng tọa độ Oxy, hypebol có 2 tiêu điểm thuộc trục hoành. Với O là trung điểm của đoạn nối 2 tiêu điểm đó, có phương trình là x^2 / a^2 - y^2 / b^2 = 1 (2) với a, b > 0.

Tương tự mỗi phương trình (2) đều là phương trình của hypebol có 2 tiêu điểm là:

F1 (-a2 + b2 ; 0) và F2 (a2 + b2 ; 0)

Tiêu cực 2c = 2a2 + b2

Giá trị tuyệt đối của hiệu khoảng cách từ một điểm thuộc hypebol đến 2 tiêu điểm sẽ bằng 2a.

Như vậy phương trình (2) được gọi là phương trình chính tắc của hypebol tương ứng.

Ví dụ:

Cho 2 phương trình x^2 / 4^2 - y^2 / 3^2 = 1 và x^2 / 5^2 - y^2 / 6^2 = -1

Ta có phương trình chính tắc của hypebol có dạng x^2 / a^2 - y^2 / b^2 = 1, với a > 0, b > 0.

Vậy nên x^2 / 4^2 - y^2 / 3^2 = 1 là phương trình chính tắc của đường hypebol.

Ba đường conic trong mặt phẳng tọa độ - Đường parabol

Cho điểm F cố định và đường thẳng cố định không đi qua F. Tập hợp các điểm M cách đều F và chính là đường parabol. Trong đó, F được gọi là tiêu điểm, là đường chuẩn và khoảng cách từ F đến gọi là tham số tiêu của parabol.

Tổng hợp lý thuyết và các bài tập ví dụ về ba đường conic trong mặt phẳng tọa độ

Xét (P) là một parabol với tiêu điểm F, đường chuẩn và cho H là hình chiếu vuông góc của F trên . Trong hệ trục tọa độ Oxy có gốc O là trung điểm của HF, tia Ox trùng tia OF. Như vậy parabol (P) có phương trình y^2 = 2px (3), với p > 0.

Phương trình (3) được gọi là phương trình chính tắc của parabol (P).

Ngược lại mỗi phương trình dạng y^2 =2px có tiêu điểm F(p/2; 0) và đường chuẩn x = -p/2.

Ví dụ:

Cho parabol (P) có dạng y^2 = x

Hãy tìm tiêu điểm F, đường chuẩn của (P)

Ta có: 2p = 1 nên p = ½

Parabol sẽ có tiêu điểm F(¼; 0) và đường chuẩn là x = -¼

Hãy tìm những điểm trên (P) có khoảng cách tới F bằng 3

Điểm M(x0; y0) thuộc (P) có khoảng cách tới F bằng 3 khi và chỉ khi y0^2 = x0 và MF = 3.

Do MF = d(M, ) nên d(M, ) = 3

Bên cạnh đó : x + ¼ = 0 và x0 = y0^2 >= 0 nên

3 = d(M,) = |x0 + ¼| = x0 + ¼

Vậy x0 = 11/4 và y0 = 11/2 hoặc y0 = -11/2

Kết luận có 2 điểm M là (11/4; 11/2) và (11/4; -11/2) thỏa mãn đề bài.

Xem thêm: Nhiệt năng là gì và những ứng dụng trong thực tế

Tổng kết

Vừa rồi là tổng hợp lý thuyết ba đường conic trong mặt phẳng tọa độ kèm ví dụ minh họa. Chúc các em có những giây phút học tập thật vui, hữu ích và luôn đạt điểm tốt trong các kỳ thi. Đừng quên theo dõi chuyên mục Khám phá của techtuts.net để cập nhật thêm nhiều nội dung bài học hay nhé!